I have been looking on some math forums and posting for a couple of days and it occurred to me that the Houdini forums should have some people who know about this stuff too. I am currently working on my MA project at SCAD and I have elected to create a tool that will allow an artist to make a history dependent distribution of an attribute over a mesh. The process I have in mind for the tool working will go like this:

• 1.Artist gives the mesh with an initial state of attributes on it, be it from prim/point attributes of from a map they have painted.
  2.I make sure all of the normals are calculated.
  3.Scatter points densely on the mesh and transfer normals and the attribute we are diffusing.
  4.Iterate over the points and measure a small neighborhood around each point to capture the point numbers for calculating over.
  5.Perform a quadratic approximation of the attribute over the neighborhood <—- This is where I am right now
  6.Calculate permeability attributes (not wanting to give away too much on this just yet)
  7.Loop: 1. Gather permeability data, 2. Calculate the permeability of each point based on float ramps which represent timelines, 3. Advect attribute
  8.Save the data to a map, which can then be used by the artist to control downstream aspects of the scene.
  I am currently having some trouble with the basic diffusion step. I am trying to get a system working which will be able to advect the attribute over the point cloud before I worry about the permeability stuff. I have a good idea what I am going to do for all of that, but this part is throwing me for a loop. I am working with this general equation: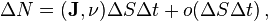
  
  Considering that the little o should be virtually 0, at this point I am considering it negligable, ΔS will be the search radius for the neighborhood generation, Δt will be 1 for all intents at this point, since it is basically just an arbitrary step in the loop. Inside the inner product, v is defined in the documentation as a normal, so I am pretty sure that should be the surface normal, which I will capture from the original geometry. The other term in the inner product is the “Flux Vector” which is what I am currently trying to figure out how to calculate. The current formula I have is: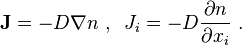
  
  Utilizing the first equation, D should be a diffusion constant which controls the speed of diffusion (as I understand it), though someone on a math forum mentioned that it could be a tensor matrix, something to look into later when I get the basic working. The real issue for me is coming from the grad(n). Since I am looking at a point cloud, which is essentially 4 dimensional at the minimum, meaning A = n(x,y,z), I am trying to figure out how to manage the partial differential calculations around the point. That is where the concept of using the neighborhood to find a quadratic approximation came from. I know that one could easily calculate the partial differentials of the approximation, but getting that approximation is proving… interesting. I am relatively sure that the advection step should be fairly straight forward as A_(t+1) = A_t + ΔN*P(x,y,z).
  
  I am not sure if I should be working in 4 dimensions, of if I should be transforming the neighborhood to the origin and projecting the points into a plane, then using the attribute as the output for a 2d mapping. Or is there an easier way to look at/solve the whole problem? I am not sure if this it the right forum to be asking this in either, but I figured that scripting was going to have the most people who might be familiar with the more theoretical aspects of how these things are produced. I am including the file I have been working in, so you can see the direction that I have been taking as well as what I have been attempting.