Math Terms for use in Houdini
12008 25 4-

- _Christopher_
- Member
- 767 posts
- Joined: 4月 2014
- Offline
-

- mark
- スタッフ
- 2619 posts
- Joined: 7月 2005
- Offline
You could try
https://www.khanacademy.org/science/physics/magnetic-forces-and-magnetic-fields/electric-motors/v/the-dot-product [khanacademy.org]
or
https://www.khanacademy.org/science/physics/magnetic-forces-and-magnetic-fields/electric-motors/v/dot-vs-cross-product [khanacademy.org]
It's a bit slow… but if you have patience, it might be helpful.
https://www.khanacademy.org/science/physics/magnetic-forces-and-magnetic-fields/electric-motors/v/the-dot-product [khanacademy.org]
or
https://www.khanacademy.org/science/physics/magnetic-forces-and-magnetic-fields/electric-motors/v/dot-vs-cross-product [khanacademy.org]
It's a bit slow… but if you have patience, it might be helpful.
Edited by mark - 2016年9月13日 09:11:54
-

- _Christopher_
- Member
- 767 posts
- Joined: 4月 2014
- Offline
Suppose I have a cube, poly split in the middle, I extrude the two faces, although not as merged faces. Isn't the angle between them a dot product ? I'm trying to understand there relation in 3D space or with anything in 3D; I know that a vector can be anywhere, but piecing it together is what is troubling me.
【T】【C】【S】
-

- edward
- Member
- 7871 posts
- Joined: 7月 2005
- Offline
Maybe try this site too:
https://betterexplained.com/articles/category/math/vector-calculus/ [betterexplained.com]
The angle is only related to the dot product. For the actual formulas, see the above link for understanding the dot product. In the special case where you have two normalized vectors (ie. they both have lengths of 1), then the dot product gives you the cosine of the angle between them.
https://betterexplained.com/articles/category/math/vector-calculus/ [betterexplained.com]
The angle is only related to the dot product. For the actual formulas, see the above link for understanding the dot product. In the special case where you have two normalized vectors (ie. they both have lengths of 1), then the dot product gives you the cosine of the angle between them.
-

- _Christopher_
- Member
- 767 posts
- Joined: 4月 2014
- Offline
It's a better site for explaining although, I don't understand the equation below as well as the Apples and Oranges analogy on the site.
What I've taken from the first part of the page is one vector can be with any math (multiplication, adding etc) can be stronger then the other vector; I still don't understand where cosine or the angle between the two vectors comes into the equation ? As well, I suppose my previous basic 3D analogy is a fail and has nothing to do with dot products ?

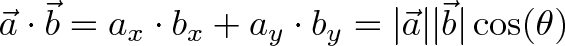
What I've taken from the first part of the page is one vector can be with any math (multiplication, adding etc) can be stronger then the other vector; I still don't understand where cosine or the angle between the two vectors comes into the equation ? As well, I suppose my previous basic 3D analogy is a fail and has nothing to do with dot products ?


【T】【C】【S】
-

- mestela
- Member
- 1795 posts
- Joined: 5月 2006
- Offline
Co-worker and all round nice guy Matt Ebb gave the best explanation for a dot product I've heard:
“Given 2 vectors, the dot product will return 1 if they're facing the same way, 0 if they're perpendicular, or -1 if they're facing opposite directions.
Vectors that aren't perfectly parallel, perpendicular, or opposite will return values between 1, 0, -1. The workings and maths behind a dot product are almost irrelevant to me; but I understand the end result and can see ways that might be useful.”
A simple example is deleting points based on their normals. Say you want to keep points that have normals that point exactly up. Up is along the y axis, so that vector is {0,1,0}. To get the dot product, in a vex wrangle you could write
dot(@N, {0,1,0} );
to make the following code a little easier to understand, I'll store that in a variable called ‘mydot’:
float mydot = dot(@N, {0,1,0} );
From what I wrote earlier, that result would have to be 1 for points that have their normal facing straight up, so we could use that in an if statement:
if ( mydot == 1 ) {
// keep those points
}
there's no vex function to keep points, but there's a function to remove points. As such, we'd reverse the test:
if ( mydot != 1 ) {
// delete points
}
but what if we wanted to keep points that are _nearly_ facing straight up? Well, if the dot product is 0 for vectors that are perpendicular, and 1 for vectors that are parallel, it follows that the dot product for nearly parallel lines will be nearly 1. Lets say if the dot product is bigger than 0.9, we'll keep those, meaning if the dot product is less than 0.9, delete them:
if ( mydot < 0.9 ) {
// delete points
}
here's the actual call you use to delete those points:
if ( mydot < 0.9 ) {
removepoint(0, @ptnum);
}
Don't sweat the details, but if you can see how comparing vectors (the normal and a vector that points down the y-axis here) can do useful things, you start to find other uses.
I tend to view the “pure maths” booklearnin' when it comes to houdini almost counterproductive when starting out. Better to have practical applications of things, then when you get comfortable, go back and learn the theory behind it. Trawl odforce and this forum for example files, the help docs for their examples, watch the masterclasses, only when you get really curious about what a quaternion actually is and how do you define a dihedral function from scratch, say, would it be time to hit the maths text books.
“Given 2 vectors, the dot product will return 1 if they're facing the same way, 0 if they're perpendicular, or -1 if they're facing opposite directions.
Vectors that aren't perfectly parallel, perpendicular, or opposite will return values between 1, 0, -1. The workings and maths behind a dot product are almost irrelevant to me; but I understand the end result and can see ways that might be useful.”
A simple example is deleting points based on their normals. Say you want to keep points that have normals that point exactly up. Up is along the y axis, so that vector is {0,1,0}. To get the dot product, in a vex wrangle you could write
dot(@N, {0,1,0} );
to make the following code a little easier to understand, I'll store that in a variable called ‘mydot’:
float mydot = dot(@N, {0,1,0} );
From what I wrote earlier, that result would have to be 1 for points that have their normal facing straight up, so we could use that in an if statement:
if ( mydot == 1 ) {
// keep those points
}
there's no vex function to keep points, but there's a function to remove points. As such, we'd reverse the test:
if ( mydot != 1 ) {
// delete points
}
but what if we wanted to keep points that are _nearly_ facing straight up? Well, if the dot product is 0 for vectors that are perpendicular, and 1 for vectors that are parallel, it follows that the dot product for nearly parallel lines will be nearly 1. Lets say if the dot product is bigger than 0.9, we'll keep those, meaning if the dot product is less than 0.9, delete them:
if ( mydot < 0.9 ) {
// delete points
}
here's the actual call you use to delete those points:
if ( mydot < 0.9 ) {
removepoint(0, @ptnum);
}
Don't sweat the details, but if you can see how comparing vectors (the normal and a vector that points down the y-axis here) can do useful things, you start to find other uses.
I tend to view the “pure maths” booklearnin' when it comes to houdini almost counterproductive when starting out. Better to have practical applications of things, then when you get comfortable, go back and learn the theory behind it. Trawl odforce and this forum for example files, the help docs for their examples, watch the masterclasses, only when you get really curious about what a quaternion actually is and how do you define a dihedral function from scratch, say, would it be time to hit the maths text books.

-

- _Christopher_
- Member
- 767 posts
- Joined: 4月 2014
- Offline
Really sweet post mestela, it did help 
How do you judge the way a vector is facing by simply previewing a point / primitive and from there you know whether it's parallel or perpendicular ?
This is going to be a crude example, but I hope it can be understood ?
?
Suppose I have a “V” shape geometry and using your delete example, except in this case I want to delete primitives. I could use the dot() function to remove all those primitives inside the “V” shape except the top faces of the “V” shape and since they are more or less considered parallel I would use the following VEX code ?
dot(@N, {1,0,0} );

How do you judge the way a vector is facing by simply previewing a point / primitive and from there you know whether it's parallel or perpendicular ?
This is going to be a crude example, but I hope it can be understood
 ?
?Suppose I have a “V” shape geometry and using your delete example, except in this case I want to delete primitives. I could use the dot() function to remove all those primitives inside the “V” shape except the top faces of the “V” shape and since they are more or less considered parallel I would use the following VEX code ?
dot(@N, {1,0,0} );
【T】【C】【S】
-

- mestela
- Member
- 1795 posts
- Joined: 5月 2006
- Offline
Don't judge or guess, visualise!
For normals, there's the ‘display normal’ and ‘display primitive normal’ buttons on the right side of the viewport. If you have other attributes, you can use the visualize sop (hotkey x) to display whatever you want, when you want.
Here I've used a normal sop to add point normals to the pig, and visualise them with the ‘display normal’ button. I then have an expanded version of the earlier code, this time with sliders to define both the spread and the vector to compare against.
For normals, there's the ‘display normal’ and ‘display primitive normal’ buttons on the right side of the viewport. If you have other attributes, you can use the visualize sop (hotkey x) to display whatever you want, when you want.
Here I've used a normal sop to add point normals to the pig, and visualise them with the ‘display normal’ button. I then have an expanded version of the earlier code, this time with sliders to define both the spread and the vector to compare against.
-

- _Christopher_
- Member
- 767 posts
- Joined: 4月 2014
- Offline
-
- anon_user_37409885
- Member
- 4189 posts
- Joined: 6月 2012
- Offline
The best way to answer the perpendicular question is to add to the Attribute Wrangle:
f@mydot = mydot;
v@myvec = myvec;
then in the Geometry Spreadsheet you can see the N, myvec and mydot values. For even more fun you can test the statement "Given 2 vectors, the dot product will return 1 if they're facing the same way"
f@mydot = mydot;
v@myvec = myvec;
then in the Geometry Spreadsheet you can see the N, myvec and mydot values. For even more fun you can test the statement "Given 2 vectors, the dot product will return 1 if they're facing the same way"

Edited by anon_user_37409885 - 2016年9月18日 02:59:26
-

- mestela
- Member
- 1795 posts
- Joined: 5月 2006
- Offline
Here's a common use for a cross product; swirling or combing normals.
The cross product if given 2 vectors will create a new one perpendicular to both. So say you have one that points down X, and one down Y, it will generate a vector that points down Z.
In this example, the first frame shows a bunch of lines copied onto points with @N from the sphere, so they stick straight out. The next frame modifies @N so that its the result of a cross between @N and a given vector. Assume that second vector was pointing along Y, and you have a line near the equator. The cross between straight up, and flat along the XZ plane will be something that sits flat on the sphere, pointing in a tangent along the equator. In fact, it will do this for all locations on the sphere, which looks like everything has been swirled around the north/south axis.
The third frame takes that result, and runs a cross product again with @N. So we have a swirl around the north/south axis, and the normal, the cross will point down, away from the north pole, towards the south pole. Again this gives a similar result for all points, resulting in a ‘combed’ look for all the lines.
The cross product if given 2 vectors will create a new one perpendicular to both. So say you have one that points down X, and one down Y, it will generate a vector that points down Z.
In this example, the first frame shows a bunch of lines copied onto points with @N from the sphere, so they stick straight out. The next frame modifies @N so that its the result of a cross between @N and a given vector. Assume that second vector was pointing along Y, and you have a line near the equator. The cross between straight up, and flat along the XZ plane will be something that sits flat on the sphere, pointing in a tangent along the equator. In fact, it will do this for all locations on the sphere, which looks like everything has been swirled around the north/south axis.
The third frame takes that result, and runs a cross product again with @N. So we have a swirl around the north/south axis, and the normal, the cross will point down, away from the north pole, towards the south pole. Again this gives a similar result for all points, resulting in a ‘combed’ look for all the lines.
Edited by mestela - 2016年9月18日 03:23:20
-

- _Christopher_
- Member
- 767 posts
- Joined: 4月 2014
- Offline
Artye
The best way to answer the perpendicular question is to add to the Attribute Wrangle:
f@mydot = mydot;
v@myvec = myvec;
then in the Geometry Spreadsheet you can see the N, myvec and mydot values. For even more fun you can test the statement "Given 2 vectors, the dot product will return 1 if they're facing the same way"
Artye - You mean to reassign the float and vector attribute mydot and myvec to simply mydot & myvec; if so I entered that into the attribute wrangler and I got an error ?
【T】【C】【S】
-
- anon_user_37409885
- Member
- 4189 posts
- Joined: 6月 2012
- Offline
Christopher R
Artye - You mean to reassign the float and vector attribute mydot and myvec to simply mydot & myvec; if so I entered that into the attribute wrangler and I got an error ?
It's best to always post your .hip file when you have an error. It's usually a simply typo.
The concept here is to visualise the data and test. Not imagine.
-

- _Christopher_
- Member
- 767 posts
- Joined: 4月 2014
- Offline
-
- anon_user_37409885
- Member
- 4189 posts
- Joined: 6月 2012
- Offline
Thanks - okay, simple one - you didn't add it to the Wrangle, you have a Wrangle with only those in there… this shows that you need to also not just learn these maths terms but understand what the Wrangle is doing.
The areas to also learn are local attributes (memory is destroyed outside of the Wrangle), global attributes (memory is preserved), using the Geometry Spreadsheet to view values, visualizer nodes to see values in the viewport.
The attached example has all this, but I've also if modified this line:
(mydot > 1-spread){removepoint(0,@ptnum);}
the ‘1-’ makes the ‘spread’ function more as it's name implies. The switch node will test against different geometries.
mestela is writing gold, so once you understand it all you are Houdini master
The areas to also learn are local attributes (memory is destroyed outside of the Wrangle), global attributes (memory is preserved), using the Geometry Spreadsheet to view values, visualizer nodes to see values in the viewport.
The attached example has all this, but I've also if modified this line:
(mydot > 1-spread){removepoint(0,@ptnum);}
the ‘1-’ makes the ‘spread’ function more as it's name implies. The switch node will test against different geometries.
mestela is writing gold, so once you understand it all you are Houdini master

-

- _Christopher_
- Member
- 767 posts
- Joined: 4月 2014
- Offline
-
- anon_user_37409885
- Member
- 4189 posts
- Joined: 6月 2012
- Offline
Christopher R
First, Artye, what do you mean I didn't add it to the Wrangle ?
Your Wrangle had nothing else but:
f@mydot = mydot;
v@myvec = myvec;
That isn't going to work as you haven't defined what mydot or myvec is… such as ‘float mydot =1;’ but the real issue is you are putting the cart before the horse. Check out tutorials such as ‘Wrangle Workshop’ https://vimeo.com/67677051 [vimeo.com] as it should help guide you more efficiently than many forum posts.
-

- mestela
- Member
- 1795 posts
- Joined: 5月 2006
- Offline
-

- _Christopher_
- Member
- 767 posts
- Joined: 4月 2014
- Offline
My mistake , now we can move ahead 
What values should mydot & myvec contain. I gave mydot a temp attribute with @N ? Although your post Artye sound as if it should have a Normal attribute ?

Artye
The best way to answer the perpendicular question is to add to the Attribute Wrangle:
f@mydot = mydot;
v@myvec = myvec;
then in the Geometry Spreadsheet you can see the N, myvec and mydot values. For even more fun you can test the statement "Given 2 vectors, the dot product will return 1 if they're facing the same way"
What values should mydot & myvec contain. I gave mydot a temp attribute with @N ? Although your post Artye sound as if it should have a Normal attribute ?
Edited by _Christopher_ - 2016年9月18日 19:52:18
【T】【C】【S】
-
- anon_user_37409885
- Member
- 4189 posts
- Joined: 6月 2012
- Offline
Christopher R
What values should mydot & myvec contain. I gave mydot a temp attribute with @N ? Although your post Artye sound as if it should have a Normal attribute ?
mydot is the result of the dot product, Houdini function = (dot(v0 , v1 )), algebraically = a(x)b(x) + a(y)b(y) + a(z)b(z)
myvec is the arbitrary vector to compare to.
At this stage you need to at least go through that page Mestala linked, as you need to understand these things, not just have knowledge of them. Also winding back and checking your knowledge of maths would be helpful. Make sure you understand Cartesian coordinates, vectors, functions and some programming.
BTW the algebra bit allows you to check things. It's not necessary per se for general usage,
-
- Quick Links





