| On this page |
Overview ¶
The deformation gradient attribute F is a 3×3 matrix that describes the local deformation. It is made up of two components:
F = Fp * Fe
Fp is the plastic component and Fe is the elastic component. The are both multiplied together to form the deformation gradient.
We only care about the Fe, as the plastic deformation (Fp) will update the rest state of the material.
Pros and cons ¶
Pros
-
It captures rotation, scaling, and shear.
-
It can also be compressed to a quaternion if only orientation is needed, to make it smaller on disk.
-
From this matrix, you can extract its determinant. You can compute the volume of the transformation and it will help you detect when the material is either compressing or when it’s stretching (
J = Jp * Je). Stretching can be associated with fracturing, so it can be very easy to drive secondary emission of debris (J).
Cons
-
The main drawback is the size (3×3 matrix is 9 floats). If you have millions and millions of points, it will be very heavy to cache on disk.

Per point local transformations - elastic component of the deformation gradient
Plastic and elastic components ¶
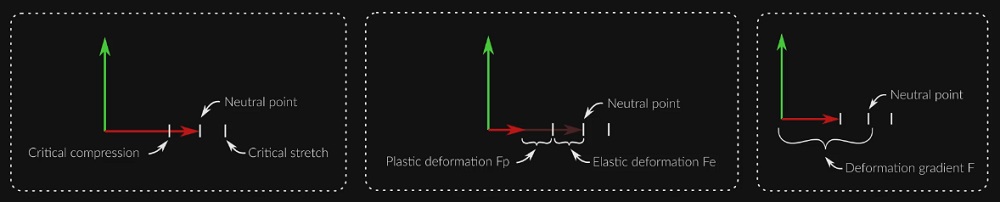
Figure 1 |
Shows a the deformation gradient with no forces applied. The first section shows the amount of critical compression and the second section shows the critical stretch along the X axis. |
Figure 2 |
A force from the right is applied and compresses the X axis. Any compression beyond the critical compression value will be considered plastic deformation. Nothing is maintained and tracked by the solver, because you're not trying to recover from it. |
Figure 3 |
On the next timestep, the solver tries to recover from only the deformation happening in the first section, and creates a new deformation gradient. |
Critical compression and critical stretch are the user defined parameters that drastically affect how the material will behave plastically or elastically.