| On this page |
このノードは、ジオメトリアトリビュートとして格納されている実行列と実ベクトルを使用して、一般的な数値線形代数演算(連立1次方程式、最小二乗法、行列の分解など)を行ない、その結果をジオメトリアトリビュートとして出力します。 このノードは、いくつかの方法でエンコードされた密行列と疎行列のどちらの入力にも対応しています。 密行列(Dense Matrix)とは、要素がすべてゼロ以外の値で埋められた行列のことで、疎行列(Sparse Matrix)とは、ほとんどの要素がゼロである行列のことです。 密行列と疎行列のどちらの線形方程式も、直接法ソルバ、または、反復法ソルバを使用して解を解くことができます。 直接法ソルバは、まず最初に、入力行列を分解し、その分解を使用して解を求めます。 反復法ソルバは、収束するまで入力行列にベクトルを何回も乗算して解を求めます。 数値線形代数の概要は、 数値線形代数 とApple社のAccelerateフレームワーク: Sparse Solversを参照してください。
このノードは、EigenとSpectraで利用可能な線形ソルバと行列の分解のクラスのラッパーとして実装されています。
TIPS
密行列に関しては、Pythonで書かれている人気のライブラリであるnumpyで、直接法ソルバを使用した同様の機能が提供されています。 あなたがnumpyに詳しいのであれば、numpyが提供しているものと、このノードのモードと直接法ソルバの選択内容とのおおまかな対比を載せた以下のテーブルを利用して、numpyからこのノードへの移行に役立てることができます。 ただし、その計算結果は、numpyとこのノードで同じになるとは限らないことに注意してください。 アプリケーションで最高のパフォーマンスを得るには、ソルバの選択とその使用方法を慎重に評価することを推奨します。 考慮すべき事項として、入力行列のサイズ、疎性、対称性、行列の分解を事前計算することで利点が得られるかどうか、反復法ソルバを使用するべきかどうかなどいくつかありますが、これらに限りません。
|
|
Mode |
Direct Solver |
|
|
Linear System Solve |
PartialPivLU |
|
|
Linear System Solve |
BDCSVD |
|
|
Decompose |
LLT |
|
|
Decompose |
HouseholderQR |
|
|
Decompose |
BDCSVD |
|
|
Decompose |
EigenSolver |
|
|
Decompose |
SelfAdjointEigenSolver |
Warning
あなた独自の問題に対して適切なソルバを選択するのは、あなたの責任です。 このノードは、指定された入力行列は、指定されたソルバを動作させるのに必要な条件(入力行列の対称性、正定値性(Positive Definiteness)、可逆性など)を満たしているかどうかをチェックしません。
Note
このノードは、x86プロセッサ上で実行する時にIntel Math Kernel Library(Intel MKL)を使用します。 環境変数を使用することで、ライブラリが高速になるように調整したり、実行する度に同じ結果が得られるようにすることができます。
入力 ¶
Matrix/Decomposition (&Vectors)
すべてのモードで演算を実行する際に使用される行列と分解を指定します。 詳細は、 Matrix を参照してください。 オプションで、2番目または3番目のジオメトリ入力が接続されていない場合に、この入力内でKnown VectorとUnknown Vectorを指定することができます。
Known Vector
Multiply モードでは、行列に乗算されるベクトルを指定します。 Linear System Solve や Solve with Decomposition モードでは、右側ベクトルを指定します。 詳細は、 Known Vector を参照してください。 2番目の入力ジオメトリが利用不可だった場合、このノードは、1番目の入力から情報の取得を試みます。 ベクトルのサイズが必要な長さの整数倍である場合、そのベクトルは、ベクトルのスタックとして再解釈され、可能であれば、そのベクトルのスタックを出力します。
Unknown Vector
Linear System Solve 、 Decompose 、 Solve with Decomposition のモードでの未知ベクトル関連の設定を指定します。 ここには、結果を累積した時のオリジナルのベクトル、そのベクトル内のピン留めされた/既知のエントリーに関する情報を含みます。 詳細は、 Unknown Vector を参照してください。 3番目の入力ジオメトリが利用不可だった場合、このノードは、1番目の入力から情報の取得を試みます。 ベクトルのサイズが必要な長さの整数倍である場合、そのベクトルは、ベクトルのスタックとして再解釈されます。
パラメータ ¶
Mode
Linear System Solve
指定された行列とベクトルに対して、選択したソルバを使用して、線形方程式系を解き、その結果のベクトルを出力します。 一部のソルバは最小二乗法にも対応しています。 利用可能なソルバの Linear Solver Setting を参照してください。
Decompose
Eigenからの直接法ソルバ、または、Spectraからの固有値ソルバのどれかを使用して、入力行列の分解を出力します。
Solve with Decomposition
Decompose モードで生成された分解とベクトルに対して、線形方程式系を解き、その結果のベクトルを出力します。 分解のタイプは入力から推測されます。
Multiply
指定された行列とベクトルを乗算して、その結果のベクトルを出力します。
Cook In-Place
このトグルを有効にすると、In-Place(コピーなし)で出力が作成されます。 無効にすると、新しいジオメトリが作成されます。
Note
In-Place出力は、入力ポイント(存在すれば)の数と入力プリミティブの数を変更することができません。 この要件が満たされなかった場合、このノードはエラーを出します。
Precision
Linear Solver SOPは、32ビットまたは64ビットの浮動小数点精度で評価することができます。
64ビットの方が精度が高いです。
Autoモードは、入力の行列/分解の優先精度に応じて32ビットと64ビットを切り替えます。
64ビット精度で実行すると、作成される浮動小数点アトリビュートは64ビットになります。
32ビット精度で実行すると、作成される浮動小数点アトリビュートは32ビットになります。
この優先精度を変更するには、Attribute Castを使用します。
Direct Solver
Linear System Solve と Decompose のモードで使用される直接法ソルバを指定します。 利用可能なソルバは以下のとおりです。
Dense
-
PartialPivLU
-
FullPivLU
-
HouseholderQR
-
ColPivHouseholderQR
-
FullPivHouseholderQR
-
CompleteOrthogonalDecomposition
-
LLT
-
LDLT
-
BDCSVD
-
JacobiSVD
BDCSVD と JacobiSVD は、特異値分解を実行します。 Decompose モードでは、特異値、それに呼応する左側のベクトル、右側のベクトルで構成された結果の3成分がポイント毎に出力ジオメトリに格納されます。
-
EigenSolver
-
SelfAdjointEigenSolver
EigenSolver と SelfAdjointEigenSolver は、固有値分解を実行します。 Decompose モードでは、固有値、それに呼応する固有ベクトルで構成された結果のペアがポイント毎に出力ジオメトリに格納されます。
これらのソルバの説明は、Eigen: Catalogue of Dense Decompositionsを参照してください。
Note
Decompose モードは、 CompleteOrthogonalDecomposition に対応していません。
Solve with Decomposition モードは、 EigenSolver または SelfAdjointEigenSolver を使用して Decompose モードで作成された分解に対応していません。
Sparse
-
LLT
-
LDLT
-
LU
-
QR
バックエンドの選択に関しては、 Backend を参照してください。
Backend
このオプションでは、 Linear System Solve モードで使用されるSparse直接法ソルバに使用されるバックエンドを選択することができます。
Note
Decompose モードは、常にEigenバックエンドで計算された分解を使用するので、このオプションは非表示になります。
Pardiso / Accelerate
このモードは、利用可能であればIntel社のPARDISOまたはApple社のAccelerateフレームで用意されている実装を使用します。 Intel社のPARDISOは、すべてのx86プラットフォームで使用され、Apple社のAccelerateフレームワークはApple SiliconのMac OSで使用されます。 Direct Solver のソルバオプションは、以下のソルバに呼応します。
Pardiso
-
PardisoLLT
-
PardisoLDLT
-
PardisoLU
-
SparseQR (Eigenの実装)
Accelerate
-
AccelerateLLT
-
AccelerateLDLT
-
SparseLU (Eigenの実装)
-
AccelerateQR
Eigen
このモードは、Eigenで用意されている実装を使用します。 Linear System Solve モードで得られる解と Solve with Decomposition モードで得られる解で整合性が取れた結果を得たい時には、このオプションを使用してください。 Direct Solver のソルバオプションは、以下のソルバに呼応します。
-
SimplicialLLT
-
SimplicialLDLT
-
SparseLU
-
SparseQR
これらのソルバの説明は、Eigen: Solving Sparse Linear Systemsを参照してください。
Use Iterative Solver
このトグルを有効にすると、直接法ソルバの代わりに反復法ソルバが使用されます。 直接法ソルバの方が精度が良いですが、メモリの消費量が多いです。 反復法ソルバは精度が悪いですが、メモリの消費量が少ないです。 したがって、一般的には、小さな問題には直接法ソルバを、大きな問題には反復法ソルバを使用することを推奨します。
Note
反復法ソルバは、 Linear System Solve モードでのみサポートされています。
Iterative Solver
入力の密行列や疎行列に対して直接法ソルバを指定します。 利用可能なソルバは以下のとおりです。
-
GMRES
-
DGMRES
-
MINRES
-
ConjugateGradient
-
LeastSquaresConjugateGradient
-
BiCGSTAB
-
IDRS
ソルバの説明は、Eigen: Iterative Linear Solvers moduleと Eigen-unsupported: Iterative Linear Solvers moduleを参照してください。
Preconditioner
反復法ソルバで使用されるプリコンディショナを指定します。 利用可能なプリコンディショナは以下のとおりです。
-
IncompleteLUT (疎行列のみ)
-
IncompleteCholesky (疎行列のみ)
LeastSquaresConjugateGradient ソルバの場合、 Diagonal プリコンディショナを選択することで、ソルバは代わりにLeastSquareDiagonalPreconditionerを使用することができます。
Solve with Guess
このトグルを有効にすると、反復ソルバは未知ベクトルを初期推定値として使用します。
Use Eigensolver
このトグルを有効にすると、直接法ソルバの代わりにSpectraライブラリの固有値ソルバが使用されます。 この固有値ソルバは、すべての固有値ペアを見つけるのではなく、一部の固有値ペアを効率的に見つけるように設計されています。 この固有値ソルバは、密行列と疎行列のどちらでも利用可能です。
Note
この固有値ソルバは、 Decompose モードでのみサポートされています。
Eigensolver
使用される固有値ソルバを指定します。 接頭辞の“Gen”は、そのソルバが一般行列用であるのに対して、接頭辞の“Sym”は、そのソルバが対称行列用であることを意味しています。
-
これらのソルバは、最大固有値ペアを指定された数だけ見つけます。
-
これらのソルバは、シフトおよび反転モードを使用して、指定されたシフトに最も近い固有値を持つ固有ペアを指定された数だけ見つけます。
各ソルバの詳細は、Spectraのドキュメントを参照してください。
Num Eigenpairs
固有値ソルバに要求する固有値と固有ベクトルのペアの数を指定します。 要求された数だけの固有値ペアをソルバが見つけることができなかった場合、このノードは警告を出します。 Spectraからのソルバは、指定された行列に対してすべての固有値ペアを見つけることができないため、このような場合には、 Direct Solver でEigenのソルバを使用することを推奨します。
Shift
GenEigsRealShiftSolver と SymEigsShiftSolver の実シフト値を指定します。
Tolerance
反復ソルバと固有値ソルバの相対誤差許容値を指定します。 許容値を小さく指定すると、ソルバの収束に時間がかかる場合があります。
Storage
ボリュームプリミティブ、Pointアトリビュート、Primitiveアトリビュート、Detailアトリビュートからの入力行列のソースを指定します。
Encoding
Volume
Dense Col-Major / Row-Major
入力の密行列は、列優先(または行優先)の順で、 Value Attribute パラメータフィールドで指定されたボリュームプリミティブとして保存されます。
行列のサイズは、ボリュームプリミティブのxとyの寸法から推測されます。
Points / Primitives
Dense Col-Major / Row-Major
入力の密行列を列優先(または行優先)の順でポイント/プリミティブ毎の配列として格納します。 これらの配列長は同じです。 列と行の数は、ポイント/プリミティブの数と配列長から推測されます。
LIL Col-Major / Row-Major
入力の疎行列をPoint/Primitiveアトリビュートとしてリストオブリスト形式(LIL)で格納します。 各ポイント/プリミティブには、列優先オプションの場合は1列(行優先オプションの場合は1行)の行エントリーが格納されます。 各列(行)には、行(列)インデックスの配列とそれに呼応した値の配列を指定する必要があります。 列数(行数)はポイント/プリミティブの数から推測されますが、行数(列数)は指定する必要があります。
Note
列方向(行方向)のポイント/プリミティブストレージを使用する代わりに、外部インデックス配列を追加で指定した場合、 この形式は、非常によく使用される圧縮Sparse列(行)形式(CSC/CSR)と同じです。
COO
入力の疎行列をPoint/Primitiveアトリビュートとして座標リスト形式(COO)で格納します。 ポイント/プリミティブ毎にスカラー、タプル、同じ長さの配列として格納される列インデックス、行インデックス、値の3成分は、行列エントリーを指定します。
Note
COOエンコードは、LILより効率が悪いです。 大きな線形方程式系には、LILを使用することを推奨します。
Detail
Dense Col-Major / Row-Major
入力の密行列を列優先(または行優先)の順でDetailアトリビュートとして平坦化された配列に格納します。 列と行の数は指定する必要があります。
COO
入力の疎行列をDetailアトリビュートとして座標リスト形式(COO)で格納します。 タプル、同じ長さの配列として格納される列インデックス、行インデックス、値の3成分は、行列エントリーを指定します。
Square Matrix
このトグルを有効にすると、行列が正方行列であると仮定して、可能な場合は常に指定されたデータから行列の形状を推測します。
Rows
エンコードから推測されない場合に、行列の行の数を指定します。
Cols
エンコードから推測されない場合に、行列の列の数を指定します。
Row Attribute
LILの列優先およびCOO疎行列形式の行インデックスを格納する整数アトリビュートの名前を指定します。 配列またはタプルを使用する時、 Col Attribute と Value Attribute も指定する必要がある場合、その配列またはタプルは、それらのアトリビュートと同じ長さである必要があります。
Col Attribute
LILの行優先およびCOO疎行列形式の列インデックスを格納する整数アトリビュートの名前を指定します。 配列またはタプルを使用する時、 Row Attribute と Value Attribute も指定する必要がある場合、その配列またはタプルは、それらのアトリビュートと同じ長さである必要があります。
Value Attribute
行列エントリーの値が格納された浮動小数点アトリビュートの名前を指定します。 配列またはタプルを使用する時、 Col Attribute と Row Attribute も指定する必要がある場合、その配列またはタプルは、それらのアトリビュートと同じ長さである必要があります。
Storage
ベクトルの格納に使用されるストレージを指定します。
Points / Primitives
入力ベクトルがPoint/Primitiveアトリビュートとして格納されます。 各ポイント/プリミティブに1つ以上のエントリーを格納することができます。 これらのエントリーは、ポイント番号/プリミティブ番号の順番で連結されて平坦なベクトルとして格納されます。
Detail
入力のベクトルが配列Detailアトリビュートとして格納されます。
Value Attribute
ベクトルエントリーの値を格納する浮動小数点アトリビュートの名前を指定します。
Storage
ベクトルの格納に使用されるストレージを指定します。
Points / Primitives
出力ベクトルがPoint/Primitiveアトリビュートとして格納されます。 各ポイント/プリミティブに1つのエントリーが格納されます。
Detail
出力ベクトルが配列Detailアトリビュートとして格納されます。
Value Attribute
ベクトルエントリーの値を格納する浮動小数点アトリビュートの名前を指定します。
Pinned Group
未知ベクトルがポイント/プリミティブとしてエンコードされている場合に、“ピン留めされた”ポイントグループ/プリミティブグループを指定します。 Linear System Solve 、 Decompose 、 Solve with Decomposition のモードでは、そのピン留めされたベクトルエントリーは無視され、 それに呼応する行列の列は計算中に除去されます。
Note
このピン情報は計算中に既知ベクトル(右手ベクトル)を修正しないので、そのような処理は別で実行する必要があります。
Note
Decompose モードでも、未知ベクトルの Value Attribute を指定することなくピン留めグループを指定して、列が削除された(そして行が削除された;以下参照)行列の分解を実行することができます。
Reduce Rows
このトグルを有効にすると、ピン留めされたグループを指定した時に呼応する列だけでなく行も削除されます。 このオプションは、正方行列に対してのみ有効です。
Scale
結果のベクトルに適用される定数スケールを指定します。
Accumulate Result
このトグルを有効にすると、計算されたベクトルと入力ジオメトリで指定されたベクトルの合計が出力されます。 スケーリングは合計の前に適用されます。
Examples ¶
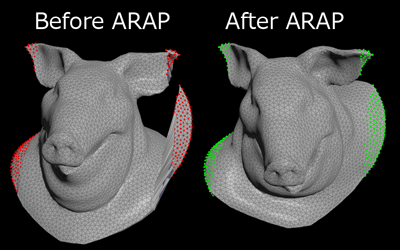
ARAPSurfaceDeformation Example for Linear Solver geometry node
このサンプルでは、Linear Solver SOPを使用してAs-Rigid-As-Possibleサーフェス変形メソッドを適用する方法を説明しています。
CurveInflation Example for Linear Solver geometry node
このサンプルでは、Linear Solver SOPを使用して、カーブで定義された入力の2次元領域を膨らまして3Dサーフェスジオメトリを作成する方法を説明しています。

RBFCageDeformer Example for Linear Solver geometry node
このサンプルでは、Linear Solver SOPを使用して、放射基底関数(Radial Basis Function:RBF)による埋め込みケージの変形に基づいてオブジェクトを変形させる方法を説明しています。

SagfreeInitialization Example for Linear Solver geometry node
このサンプルでは、Linear Solver SOPを使用して、オブジェクトが重力によってたわまないようにVellum距離拘束を初期化する方法を説明しています。

| See also |